이 포스팅은 도서 개발자를 위한 실전 선형대수학에 대한 리뷰를 담고 있습니다.

- 출처: 한빛미디어
요약
선형대수(linear algebra)는 데이터분석 혹은 기계학습을 학습하는데 있어 기초를 탄탄하게 할 수 있는 기초 중 하나입니다. 실제로 어떻게 쓰이는지 예시를 본다면 다음과 같습니다.
첫째로 딥러닝을 통한 임베딩 스페이스를 발견하기 전에는 단어와 문서 사이에 보이지 않는 관계를 가정하여 pLSA (probabilistic Latent Semantic Analysis) 라는 방법을 사용했습니다. 좀 더 쉽게 설명하자면 각 문서가 어떤 토픽으로 구성되었나 하는 것들을 분석하기 위해서 이러한 작업을 했다고 생각하시면 됩니다. 이 책에서는 pLSA의 기반이 되는 특이값 분해 (Singular Value Decomposition)을 설명하고 있습니다.
둘째로 바로 앞에 언급한 임베딩 스페이스에서는 서로간의 유사성을 측정하기 위해 코사인 유사도를 사용하는데 이 책에서 설명하고 있는 벡터-내적 연산을 활용합니다.
이 외에도 선형대수의 기초적인 개념은 다양한 곳에서 쓰이고 있습니다. 이 책은 선형대수에서 중요한 핵심 개념들을 설명하고 있는데 어떤 분야를 공부하기 위해 선형대수를 보게 되었는지 생각하시면서 이 책을 보신다면 더욱 도움이 될 것이라 생각합니다. 물론 선형대수 자체에 흥미를 느껴 이를 탐구하고자 할 때에도 좋은 책이라 생각합니다. 파이썬의 numpy 라이브러리와 함께 잘 설명하고 있기에 추후 데이터 분석 혹은 기계학습 모델링을 할 때 기초가 부족하여 막히는 경우는 없을만큼 내용이 잘 정리된 책이라 생각합니다.
선형대수가 왜 필요한가?
개발자를 위한 실전 선형대수학 책의 목차를 보면 기초 연산부터 고급 개념 - 고윳값, 특이값 - 까지 설명과 예시가 촘촘하게 구성되어 있습니다. 그러면 선형대수를 왜 공부해야 할까요?
우리가 세상을 해석하는데 여러가지 관점이 있을 수 있는데 선형대수의 경우 정량적인 방법을 통해 무엇이 중요한지 알 수 있게 해주는 방법이 있기에 알아야 한다고 생각합니다. 예를 들어 특정 이미지에 대해 고윳값 분해를 통해 핵심 정보만 남기더라도 원본 이미지와 상당히 유사한 결과를 얻을 수 있습니다.
PCA의 경우 1909년 고안된 방법입니다. 위키 PCA 또한 주어진 문제를 해결하는 과정에서 나온 방법일 것 이기에 선형대수의 원리와 기초를 잘 터득하고 있다면 우리도 이를 응용하여 필요에 맞게 도구를 활용할 수 있을 것 입니다.
물론 딥러닝을 통한 embedding space가 워낙 강력하기에 product 레벨에서 직접적인 사용은 어려울 수 있으나 우리가 나름대로 데이터를 이해하고 세상을 받아들이는데 있어 도구를 하나 더 갖춘다는 것은 손해보는 일이 아닐 것이라 생각합니다.
이러한 점들을 종합적으로 고려한다면 데이터 수치를 정량적인 관점에서 볼 수 있게 해주는 선형대수를 공부하는 것은 나쁘지 않다 생각합니다. 또한 이 책은 머신러닝에서 반드시 사용되는 파이썬과 numpy를 통해 개념을 설명하고 있기에 선형대수에 대한 기초를 쌓고자 하는 분들에게 추천합니다.
기초 연산
이 책은 벡터가 무엇인지부터 설명하고 있는데 numpy로 표현하면 아래와 같이 간단합니다.
import numpy as np
v = np.array([4,5,6])
그리고 두개의 벡터 v, w가 있다고 할 때 이에 대한 덧셈과 뺄셈은 아래와 같습니다.
import numpy as np
v = np.array([4,5,6])
w = np.array([7,8,9])
vw1 = v + w
vw2 = v - w
이러한 연산이 물리적으로 어떤 의미를 갖는지 이해하고 넘어가는 것은 상당히 중요합니다. 이 책을 보면 아래와 같이 기하학적 해석이라고 되어있는데요, 이 그림만으로 물리적 의미를 해석하기는 어렵겠지만 알고자 하는 데이터를 대입하여 분석하시면 더욱 의미가 있을 것 입니다.
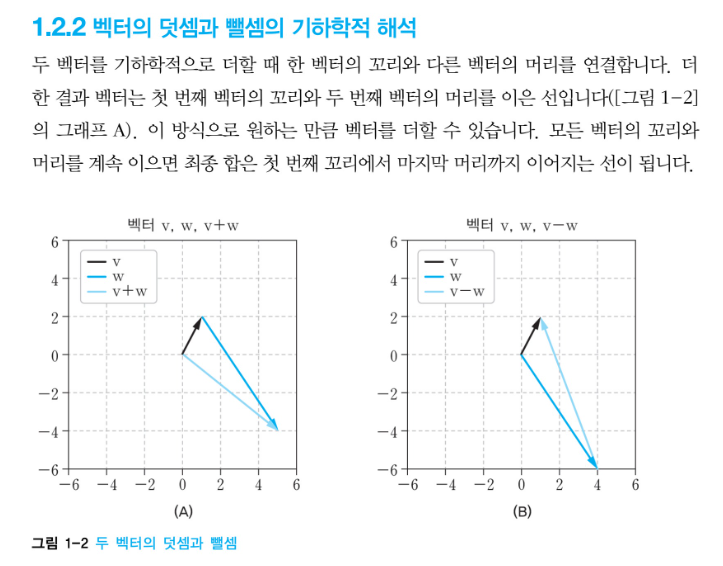
- 출처: 한빛미디어
고윳값 분해 그리고 주성분 분석 (PCA)
앞서 공유드린 예시를 다시 한번 살펴보겠습니다.
원본 이미지

- 출처: https://scicoding.com
압축 이미지

- 출처: https://scicoding.com
위의 압축 이미지 예시에 나온 6개의 이미지는 이미지 데이터를 PCA라는 방법을 통해 주요 차원을 추출하여 주요 차원의 갯수를 점차 늘려나갔을 떄의 효과를 보여주고 있습니다. 여기서 우리가 생각해보면 좋은 점은 단순히 PCA라는 방법론에 대한 이해가 아니라 이러한 방법이 왜 필요했을지 입니다. 컴퓨터 초창기만 하더라도 이미지 한개의 데이터를 송수신하는 것은 굉장히 느리고 어려운 작업이었습니다. 여기서 저의 상상을 덧붙이자면 이미지 원본을 그대로 보낼 것이 아니라 중요한 정보만 보내고 나머지는 버리도록 하여 제한된 네트워크 자원을 효율적으로 쓰는 것이 중요하기에 위와 같은 방법을 활용하지 않았을까 생각합니다.
마무리
데이터분석 혹은 모델 학습을 할 때 선형대수는 반드시 알고 있어야 할 기초 중 하나입니다.
이 책에서는 벡터의 기초부터 SVD와 PCA까지 파이썬과 numpy를 통해 상세히 그리고 실용적으로 설명을 하고 있습니다.
책을 보면 중간중간 실제 예시를 들며 설명을 하고 있습니다.
예를 들면 이미지 특징 탐지 혹은 날씨에 따른 자전거 대여량 예측 등과 같이 실제 사용될 만한 예시를 들고 있습니다.
책의 내용과 구성이 선형대수의 기초를 이해하기에 잘되어 있기에 각 챕터를 읽으시며 numpy로 구현 후 각자 푸시고자 하는 문제라면 어디에 활용할 수 있을지 고민하시면서 진행하신다면 좀 더 많은 것을 얻으실 수 있을 것이라 생각합니다.
한빛미디어 <나는 리뷰어다> 활동을 위해서 책을 제공받아 작성된 서평입니다.